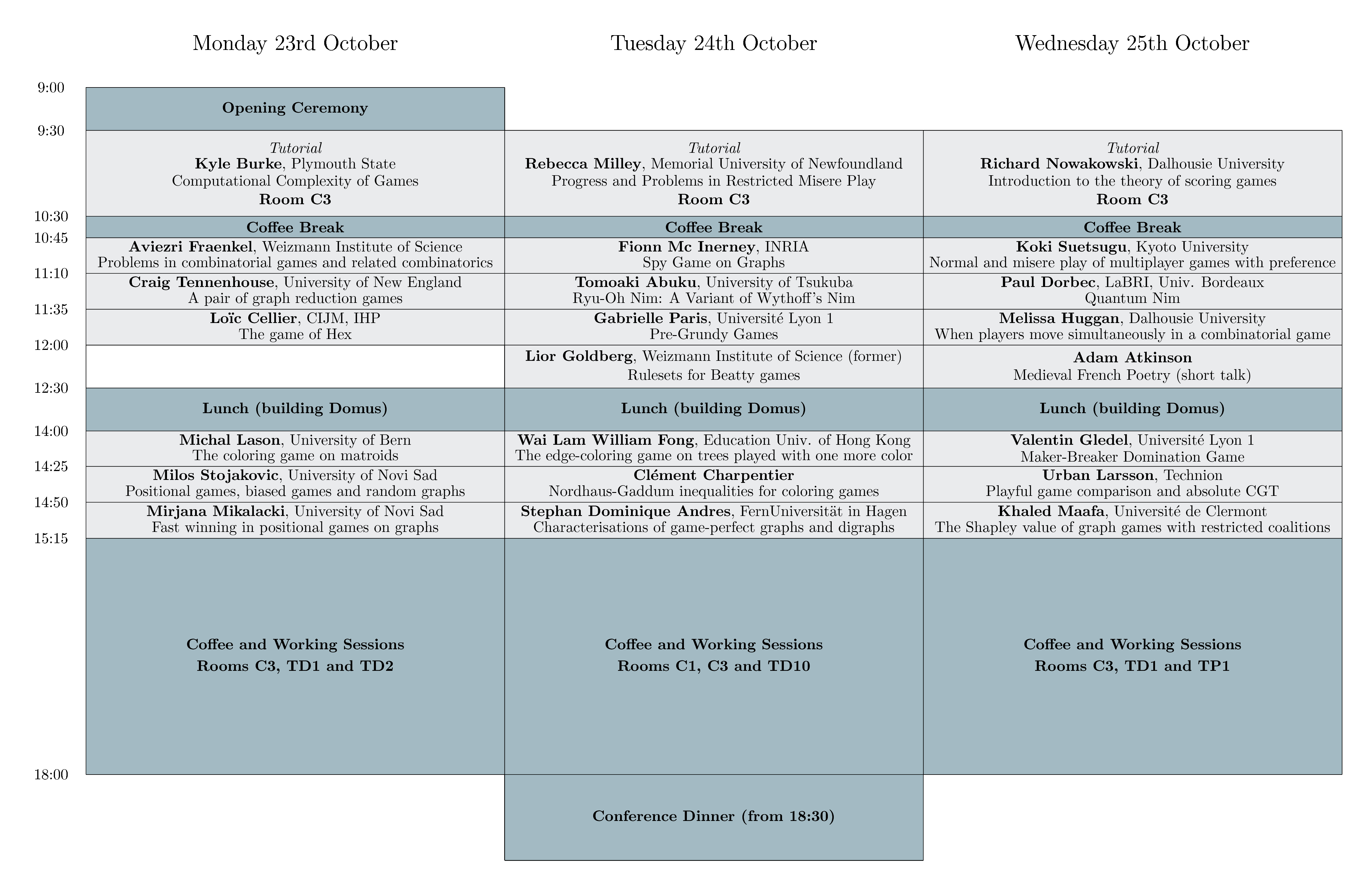
GAG Workshop Program
The talks in the morning, and the beginning of the afternoon will take place in room C3 , on the ground floor of building Nautibus. In the afternoon, the working sessions will be in rooms:
- C3, TD1 and TD2 on Monday,
- C1, C3 and TD10 on Tuesday,
- C3, TD10 and TP1 on Wednesday.
Tutorials
Topic: Introduction to the theory of scoring games
Abstract:
A coherent theory of combinatorial scoring games has been developed in the last 4 years. This theory extends the theory of Normal play games found in 'Winning Ways' in a natural fashion. Unfortunately, the reduction to canonical form is trickier. With hindsight, we also see that some graph theorists have been using scoring games to obtain bounds on some graph parameters. I will give a tutorial on scoring games, using lots of examples, and mention briefly some of the previous graph theory questions.
Topic: Progress and Problems in Restricted Misere Play – [Slides]
Abstract:
Misere games, where the last player to move loses, are notoriously harder to analyze than normal-play games. For example, no non-zero game is equal to zero in general misere play, and so there are no inverses and no easy test for equality or inequality. Misere research was accordingly scarce until Plambeck and Siegel's (2005, 2008) indistinguishability theory excited new interest in misere play: now we can consider two games indistinguishable (equivalent) modulo a restricted set (universe) of games, even if they are not equal in general. This talk will provide the necessary background for working in restricted misere play and will discuss recent developments in the comparison, reversibility, and invertibility of games modulo general and particular restricted universes. Open problems in these and other areas will be discussed.
Topic: Computational Complexity of Games – [Slides]
Abstract:
This talk provides an overview of algorithmic combinatorial game theory, the application of computational complexity to CGT. We first explain computational complexity and reductions. Then we'll explain the importance of this in CGT. We'll discuss how complexity results can evolve for the same ruleset and show some classic examples, ending with open problems.
Talks
Monday
Title: Problems in combinatorial games and related combinatorics.
Title: A pair of graph reduction games
Abstract: We introduce two graph games, one a variant of Hackenbush with many hot positions and another based on a deletion/contraction mechanic. We show that the latter game is highly atomic in a very visible way, and demonstrate a linear time algorithm to determine the value of a position.
Title: The game of Hex - historical aspects, variants of the rules, and first properties
Abstract: The game of Hex is a combinatorial game, which was discovered in 1942 by Piet Hein, Danish scientist and poet, and presented again in 1948 by John F. Nash, a North-american mathematician. It is a connection game on a hexagonal tiling. We present historical aspects of this game, with graph theory and computational complexity. We propose some variants of the rules; and, we discuss first properties, for instance, who owns the winning strategy for some configurations.
Title: The coloring game on matroids
Abstract: A coloring of the ground set of a matroid is proper if elements of the same color form an independent set. For a loopless matroid, its chromatic number is the minimum number of colors in a proper coloring. We study a game-theoretic variant of this parameter.
Suppose that Alice and Bob alternately properly color the ground set of a matroid M using a fixed set of colors. The game ends when the whole matroid has been colored, or if they arrive at a partial coloring that cannot be further properly extended. Alice wins in the first case, while Bob in the second. The game chromatic number of M is the minimum size of the set of colors for which Alice has a winning strategy. Clearly, the game chromatic number is greater or equal to the chromatic number.
We prove an almost tight (up to 1) upper bound for the game chromatic number of a matroid in terms of its chromatic number.
Title: Positional games, biased games and random graphs
Abstract: We introduce the concept of a positional game, with accent on Maker-Breaker games. Then we move on to analyzing biased games on graphs, and games on random graphs. Special attention will be devoted to numerous open problems that we encounter en route.
Title: Fast winning in positional games on graphs
Abstract: We look at positional games on graphs, with focus on Maker-Breaker games. For some standard graph games, for which the winner is known, we are curious about how fast one can win. We consider both unbiased and biased games and analyse their duration. Finally, we present some related open problems.
Tuesday
Title: Spy Game on Graphs – [Slides]
Abstract: We present a generalization of the Eternal Domination Game called the Spy Game. A spy moves at speed $s \geq 2$ in a graph in the search of a vertex that is distance at least $d + 1$ from all the guards (speed 1) who want to control him (i.e. assure that there is always at least 1 guard at distance at most d from the spy). The objective is to minimize the number of guards (guard number) while ensuring they can eternally control the spy. We present results in various classes of graphs.
Title: Ryu-Oh Nim: A Variant of Wythoff's Nim – [Slides]
Abstract: We study Ryu-Oh Nim, an impartial game played using a Ryu-Oh instead of a queen in Wythoff's Nim. A Ryu-Oh (meaning the Dragon King) is a piece in shogi (Japanese chess) which can make a movement combining those of a king and a rook in chess.
We give the Grandy values for Ryu-Oh Nim and its several generalized versions. We also study the 3-dimensional version of Ryu-Oh Nim.
Title: Pre-Grundy Games – [Slides]
Abstract: Pre-Grundy games are a subclass of hexadecimal games where the players are not allowed to remove tokens. Inspired by the Grundy game, where the players take turns to split a $n$-sized heap in a given number of heaps of different sizes, the Pre-Grundy games remove this different-size constraint. Here we give an adapted version of the periodicity check on octal games, and prove that a few easy to check conditions suffice to prove the periodicity of a pre-Grundy game. Furthermore, we find the exact sequence of most pre-Grundy families.
Title: Rulesets for Beatty games – [Slides]
Abstract: It is known that the P-positions of Wythoff are given by two complementary homogeneous Beatty sequences. So are the P-positions of its generalized version, t-Wythoff.
We show how to find an explicit ruleset for 2-piles invariant games with P-positions given by an arbitrary pair of complementary homogeneous Beatty sequences.
We also give a criterion whether such a pair has a ruleset that is a finite modification
of t-Wythoff.
Joint work with Aviezri S. Fraenkel.
Title: The edge-coloring game on trees played with one more color – [Slides]
Abstract: In an edge-coloring game, Alice and Bob alternately choose one color from a set of k colors and put it on an uncolored edge of a graph G under the constraint that no two adjacent edges receive the same color. Alice wins if all the edges of the graph can be colored; otherwise, Bob does. The least k such that Alice has a winning strategy is the game chromatic index of G. We prove that Alice can win the game on any tree with a set of k’ colors if k’ is not less than the game chromatic index of the tree.
Keywords: game chromatic index, tree
Title: Nordhaus-Gaddum inequalities for coloring games – [Slides]
Abstract: A seminal result by Nordhaus and Gaddum gives upper and lower bounds for the sum of the chromatic number of a graph and its complement. We provide similar results for the chromatic and coloring game numbers.
Title: Characterisations of game-perfect graphs and digraphs – [Slides]
Abstract: A graph $G$ is game-perfect if the game chromatic number of any induced subgraph $H$ of $G$ equals the clique number of $H$. We characterize game-perfect graphs for the games $g_A$ resp. $g_B$ where the maker resp. the breaker has the first move and missing a turn is not allowed by a set of 7 resp. 15 forbidden induced subgraphs. Notions of game-perfectness can be generalized in two ways to digraphs. We reduce the characterization of weakly game-perfect digraphs to the undirected case. Furthermore, we prove that strongly game-perfect digraphs w.r.t. game $g_A$ have a kernel. This is joint work with Edwin Lock.
Wednesday
Title: The normal play and the misere play of multiplater games with preference – [Slides]
Abstract: In order to analyze multiplayer CGT, we need to consider the objectives of players that are guaranteed to lose. In this presentation, we assume each player has a fixed "preference", which is defined as a total ordering of the every players(including herself), and each player's preference is known by all other players. Each player behaves so that the winner will have the highest possible preference value. We present solutions for various forms of preferences in multiplayer game which include the generalization of the normal play and the misere play.
Title: Quantum Nim
Abstract: In this talk, we propose a Quantum variation of combinatorial games, generalizing the Quantum Tic-Tac-Toe proposed by Allan Goff [2006]. We consider the possibility of playing superpositions of moves. We propose different rulesets depending on when superposed moves should be played, and prove that all these rulesets may lead similar games to different outcomes. We then consider Quantum variations of the game of Nim. We conclude with some discussion on the relative interest of the different rulesets.
Title: What happens when players move simultaneously in a combinatorial game?
Abstract: This talk explores different interpretations for playing combinatorial games with simultaneous moves. Examining the overlap between economic game theory and combinatorial game theory, we begin developing possible directions for the theory of simultaneous combinatorial games.
Title: Medieval French Poetry – [Slides]
Abstract: This short (a few minutes) talk will showcase a small volume of medieval French poetry which is not as well known as perhaps it should be. People who wish to examine it in more detail can do so during breaks.
Title: Maker-Breaker Domination Game
Abstract: The Maker-Breaker Domination game is played on a graph G. Two players, Dominator and Staller, alternatively select a vertex previously unselected. Dominator wins if the vertices he selected form a dominating set and Staller wins if Dominator is unable to form such a set, i.e. if there exists a vertex such that himself and all its neighbors are selected by Staller. This game can also be seen as instances of the POS-CNF game introduced by Schaefer.
We prove that this game is PSPACE-complete on split graphs and bipartite graphs, and that it is polynomial solving on trees and cographs.
Title: Playful game comparison and absolute CGT – [Slides]
Abstract: In two recent manuscripts, we develop an encompassing theory for many universes of combinatorial games, including normal-play, misere-play and scoring-play. The universe can be any restriction of a free space of games, provided it is parental and dense. Parental means that, if games $G$ and $H$ belong to the universe, then the game $\langle G\mid H\rangle $ belongs to the universe. Dense means that, for any outcome $x$, and any game $G$, then there is a game $H$ such that $o(G+H) = x$. If a universe is both parental and dense, then it is an \emph{absolute universe}. For games $G$ and $H$ in any absolute universe, we discuss how a dual normal-play strategy on the ordered pair of games $[G, H]$, gives a constructive answer to the question: is $G\ge H$? This is joint work with Santos and Nowakowski.
Title: Computing the Shapley value of graph games with restricted coallitions. – [Slides]
Abstract: We study algorithms for the computation of the Shapley value of a cooperative game on a lattice. We show that, when the lattice is isomorphic to a product of chains and the game is a weighted graph game, the Shapley value can be computed in polynomial time, provided that the length of the chains is fixed.
|

|

|

|