Isochrones: démarche exploratoire, seconde et dernière partie

Note:

On reprend les mêmes paramètres que dans l’article précédent en ajoutant une adresse supplémentaire pour pouvoir visualiser des intersections après avoir vu comment on pouvait améliorer les isochrones produits.

  • durée maximale: 20 minutes
  • adresse de départ: “90, Boulevard Saint-Germain, 75005, France”, “334, Rue des Pyrénées, 75020, France”
  • date: Jour ouvrable type
  • heure de départ: 08:00
  • API: Navitia (journeys)

Comme on l’a vu, il est nécessaire de tester d’autres formes d’isochrones afin d’affiner les résultats.

Améliorer l’isochrone

Récupérer le réseau viaire

Afin de prendre en compte le réseau viaire (dans notre exemple, celui de Paris), il convient de le récupérer et de le transformer en graphe afin qu’on puisse calculer des plus courts chemins à pied en fonction du temps restant à destination à chaque station - de transports en commun - accessible. Pour faire simple, nous n’allons plus tracer des buffers autour des stations mais des chemins les plus courts sur le réseau empruntable à pied.

Cela paraît peut-être un peu compliqué mais grâce aux possibilités offertes par la librairie Python OSMnx, il est assez aisé de récupérer les données d’OpenStreetMap et de les transformer en graphe. C’est pour cette raison que nous utilisons cette librairie au sein de nos propres modules.

Nous récupérons donc tout d’abord le graphe de la région parisienne et nous créons des fichiers de noeuds et d’arcs au format JSON (afin de pouvoir les stocker et ainsi les réutiliser comme bon nous semble et en les chargeant très vite car la récupération en ligne des données peut se révéler assez lente.), comme on le montre dans le notebook.

Ce réseau va être utilisé notamment pour générer des plus courts chemins qui prendront la forme de multilignes auxquelles nous allons donner une certaine épaisseur afin de procéder à quelques manipulations spatiales. Mais tout d’abord, faisons un point théorique sur les opérations spatiales.

Point sur les opérations spatiales

La carte que nous présentons dans le notebook comporte différentes couches (cliquer dessus dans la légende permet de les faire disparaître/apparaître sur le fond cartographique) qui correspondent à différentes opérations spatiales, notamment permise par GeoPandas que nous utilisons également au sein de nos propres modules Python.

L’idée est de réaliser des isochrones basés sur la méthode présentée dans le billet précédent mais également d’en créer d’autres avec l’appui de calculs tenant compte du réseau viaire et de procéder à quelques opérations spatiales afin de mettre en évidence, par exemple, les vides et les pleins.

Pour expliciter notre démarche, attardons nous sur le schéma suivant (basé sur la documentation GeoPandas). La situtation initiale - nous faisons simples ici mais les exemples présentés après sont beaucoup plus complexes en termes de géométries - comporte deux polygones (un cercle et un carré). Nous présentons 4 opérations spatiales (cf. figure ci-après):

  • intersection: ce qui est commun au cercle et au carré
  • différence symétrique: tout sauf ce qui est commun au carré et au cercle, c’est l’inverse de l’intersection
  • union: à la fois le carré et le cercle
  • différence: carré auquel est soustrait ce qui correspond à l’intersection entre le carré et le cercle ou cercle auquel est soustrait ce qui correspond à l’intersection. Tout dépend de la façon dont est appliquée cette opération spatiale.

</a>

Nous allons voir comment appliquer ces possibilités d’opérations spatiales sur nos exemples d’isochrones.

Affiner, préciser, diversifier les isochrones

Cliquez sur l’image pour accéder à leur version dynamique et interactive dans un notebook Jupyter

Nous nous basons pour partie sur les méthodes et les exemples exposés par Geoff Boeing et Kuan Butts qui utilisent la librairie OSMnx pour créer diverses visualisation isochrones.

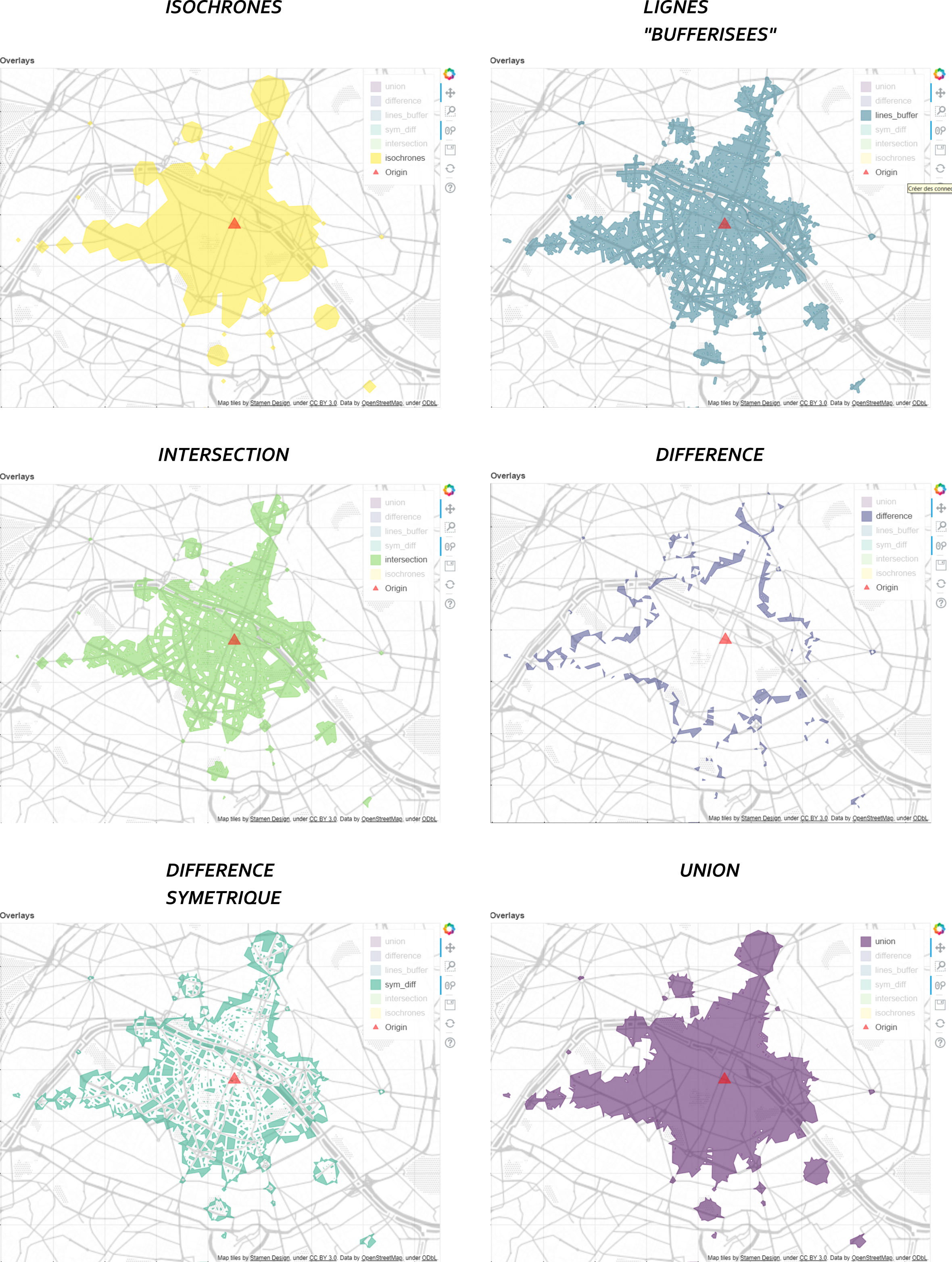
Nous avons créé plusieurs couches (cf. image ci-après ainsi que la version interactive en cliquant sur l’image):

  • Isochrones => Isochrones (comme le propose l’API Navitia mais dans une version simplifiée pour effectuer plus rapidement des opérations spatiales)
  • Lines_buffer => Lignes bufferisées (nous calculons les plus courts chemins entre une origine et tous les noeuds du réseau dans un temps et une heure donnés et nous créons des isochrones basés sur le réseau viaire en fonction du temps restant à destination)
  • Intersection => Intersection entre les isochrones et les lignes bufferisées (ce qui est commun aux deux couches)
  • Difference => Différence entre les isochrones et les lignes bufferisées (ce qui reste de la soustraction entre les deux couches)
  • Sym_diff => Différence symétrique entre les isochrones et les lignes bufferisées
  • Union => Union des isochrones et des lignes bufferisées

Mise en évidence des intersections

Cliquez sur l’image pour accéder à leur version dynamique et interactive dans un notebook Jupyter

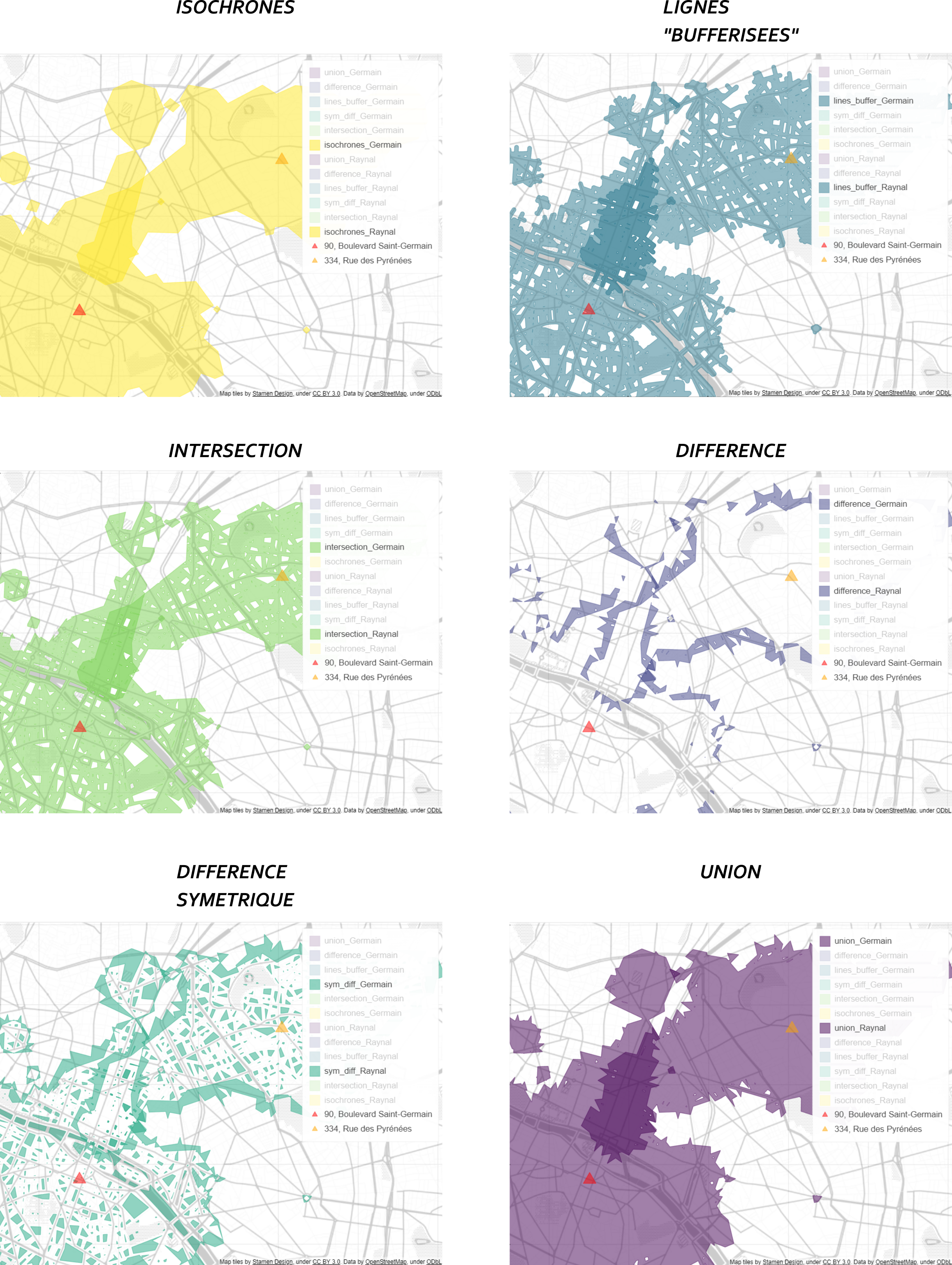
L’ajout d’une autre origine - puisque, souvenez-vous, vous souhaitez connaître la zone optimale de rencontre pour votre ami et vous-mêmes - permet de mettre en évidence l’existence ou non de superpositions spatiales en fonction des méthodes choisies.

La figure suivante (et sa version dynamique) montre une plus ou moins grande facilité à voir les superpositions en fonction des opérations spatiales. Les couches d’isochrones, des lignes "*bufferisées*", des intersections et unions permettent d’identifier plus rapidement les zones de rencontres possibles. Les lignes "*bufferisées*" semblent moins facilement lisibles que les autres mais elles sont plus précises.

Les couches de différences et de différences symétriques apparaissent utiles pour mettre en avant les obstacles naturels et artificielles mais à l’échelle d’une origine. Elles ne sont pas très lisibles pour mettre en avant les intersections éventuelles.

Il est à noter qu’il serait possible également d’utiliser des couleurs différentes pour chaque adresse afin de faire apparaître une autre couleur (fruit de l’union de deux couleurs, par exemple rouge et bleu donnant du violet) lors des supersositions/intersections.

Voilà, il ne vous reste plus qu’à trouver un point de rendez-vous dans les zones mises en évidence, le choix de la technique dépendant de l’importance accordée à divers critères: lisibilité, précision, …

Bien entendu, il ne s’agit que de zones de rencontre possibles pour un moment bien précis dans la journée avec une contrainte sur l’heure de départ et le temps passé. Pour améliorer ces résultats, il faudrait mettre en place une version dynamique afin de voir l’évolution de ces zones au fur et à mesure du temps qui s’écoule dans une journée avec, par exemple, un intervalle de 10 minutes.