Montrer l’accessibilité par l’isochrone

Pourquoi, comment ?

Imaginons que vous souhaitiez connaître tous les restaurants, servant des petits déjeuners, accessibles (à pied et en tranports collectifs) depuis votre domicile en début de matinée.

Une première possibilité consiste à ouvrir un site ou une application de géolocalisation et à taper “restaurant” pour trouver les établissements à proximité et à choisir le plus proche. Dans ce cas, rien de bien sorcier. Mais se cantonner à ce cas signifierait arrêter ici ce billet et avouons-le, ce serait bien dommage (ou, en tout cas, prétendons que ça le serait).

Envisageons donc que vous désiriez connaître tous les restaurants accessibles car ils ne proposent pas, par exemple, tous les mêmes menus et peuvent chacun avoir des spécificités intéressantes.

Une première méthode consiste à tracer un cercle à vol d’oiseau (d’une certaine distance / rayon) et à regarder ce qui est accessible. Mais cela ne rend pas compte des zones réellement accessibles avec vos contraintes: l’utilisation des transports collectifs qui sont soumis à des horaires et le fait que vous ayez vous-mêmes des contraintes temporelles. Il vous faut donc savoir ce qui est accessible dans un espace-temps particulier (sans pour autant devoir voyager à 88 miles à l’heure …) en tenant compte de ces contraintes. C’est ici qu’intervient l’accessibilité mesurée par le calcul des plus courts chemins via un ou des graphes et transposée en polygone(s) isochrone(s).

Un petit point définition s’impose.

Point définitions

Accessibilité:

“Plus ou moins grande facilité pour accéder à un lieu en vue d’y effectuer une activité”, (source: article L. Chapelon)

Isochrone:

“du grec isos, égal, et khronos, temps” (source: Larousse)

Graphe:

Ensemble de nœuds (vertices) et d’arcs (edges) liant certains certains nœuds. Dans le cadre de notre approche, le graphe (routier, pédestre, cyclable, de transport collectif, …) est:

Il est donc question de mesurer l’accessibilité en tenant compte de l’espace mais aussi du temps, ce qui implique - dans notre cas qui comporte un déplacement en transports collectifs - des horaires, des distances et des durées de déplacements. Il s’agit non pas de connaître l’accessibilité théorique (cercle correspondant à une distance-temps à vol d’oiseau) mais bien l’accessibilité réelle (les lieux accessibles dans un espace-temps donné et contraints par des horaires et des modes de déplacement).

Ces quelques précisions étant faites, nous pouvons nous lancer dans ce petit billet sur l’accessibilité et les isochrones, et si quelques éléments vous paraissent encore obscurs, pas d’inquiétude, nous allons essayer de les éclaircir autant que faire se peut.

Calculer et représenter l’accessibilité ?

L’accès à des lieux peut être réalisé en utilisant différents modes de transport (marche à pied, transports collectifs, véhicule motorisé individuel, véhicule non-motorisé individuel) et diverses combinaisons de ces modes (le déplacement peut être monomodal ou intermodal).

La mesure de cette accessibilité varie en fonction des modes empruntés. En effet, les modes individuels motorisés ou non motorisés vont être soumis aux règles de circulation et au trafic, tandis que les transports collectifs sont, en plus, contraints par des horaires (même pour les modes à haute fréquence comme le métro ou le tramway, entre autres). Pour effectuer des mesures, il faut créer un ou plusieurs graphes (nous ne développerons pas ce point dans ce billet de blog) et calculer les plus courts chemins entre des origines et des destinations.

Vol d’oiseau et plus court chemin: du cercle au polygone isochrone

Il est question de réaliser des calculs sur des graphes avec des algorithmes du plus court chemin. Les lignes de transports collectifs (stations, horaires, …), les tronçons routiers (vitesse constatée, vitesse limite autorisée, distance, …) sont traduits en arcs et en nœuds pour former ces graphes.

Les mesures de l’accessibilité permettent de connaître les nœuds accessibles depuis un nœud d’origine en un temps donné avec une potentielle contrainte sur l’heure d’arrivée ou l’heure de départ.

Sans utilisation de graphe, mesurer l’accessibilité de manière la plus simple - pour connaître l’espace “accessible” - passe par l’élaboration d’un polygone basé sur une distance-temps à vol d’oiseau comme on le précisait au début de notre article:

  • on estime une vitesse moyenne (exemple: 15km/h à vélo, soit 15 000 mètres parcourus en une heure, car nous aavons besoin d’un résultat en mètres pour construire notre zone tampon / cercle)
  • on décide d’un temps de déplacement maximum (exemple: 20 minutes)
  • on trace un cercle d’un rayon calculé à partir de la vitesse et du temps (20x15000/60=5000 mètres)

La figure animée ci-dessous montre le passage d’une accessibilité théorique à vol d’oiseau à une accessibilité réelle tenant compte des contraintes du réseau viaire (le tracé des rues empruntables par un mode spécifique avec toutes les contraintes: limites physiques comme les cours d’eau, contraintes légales comme les vitesses maximales autorisées, …) et calculée grâce à des algorithmes de plus court chemin. Dans l’illustration, on déforme, chiffonne petit à petit le cercle pour montrer qu’il doit se contraindre aux différentes limites d’accès. Ce dernier prend finalement la forme d’un polygone isochrone tenant compte des contraintes du réseau.

Le multidigraphe des transports collectifs

Dans le cadre de notre étude, nous nous sommes penchés sur l’accessibilité en transports collectifs. Ces modes sont fortement contraints par des horaires et demandent l’élaboration de graphes plutôt complexes. En effet, chaque nœud du graphe peut être relié par plusieurs arcs (en fonction des modes et des horaires). Par exemple, deux pôles d’échange peuvent être reliés par une ligne de métro, de tramway et de bus et cela à des horaires précis tout au long de la journée; le graphe doit donc comprendre tous les arcs possibles.

Le schéma ci-avant illustre les différences entre un graphe routier et un graphe de transport collectif. L’exemple en bas de l’illustration permet de montrer les changements de modes lors d’un trajet multimodal en transports collectifs. Cela met en évidence une des constructions possibles d’un multidigraphe:

  • 1 niveau par mode
  • Des arcs pour relier chaque mode à certain nœuds
  • Des arcs pour relier le ou les graphe(s) de TC au réseau viaire
  • Le graphe du réseau viaire
  • Des arcs multiples entre chaque nœud (il est possible de créer un arc pour chaque trajet entre deux stations ainsi que pour chaque mode)

Cela implique une différence de représentation entre le tracé des lignes de TC et le graphe, comme le montre la figure ci-après (le fond de carte représente une partie de la ville de Lille mais les tracés et le graphe sont fictifs).

Des mesures de l’accessibilité à l’isochrone

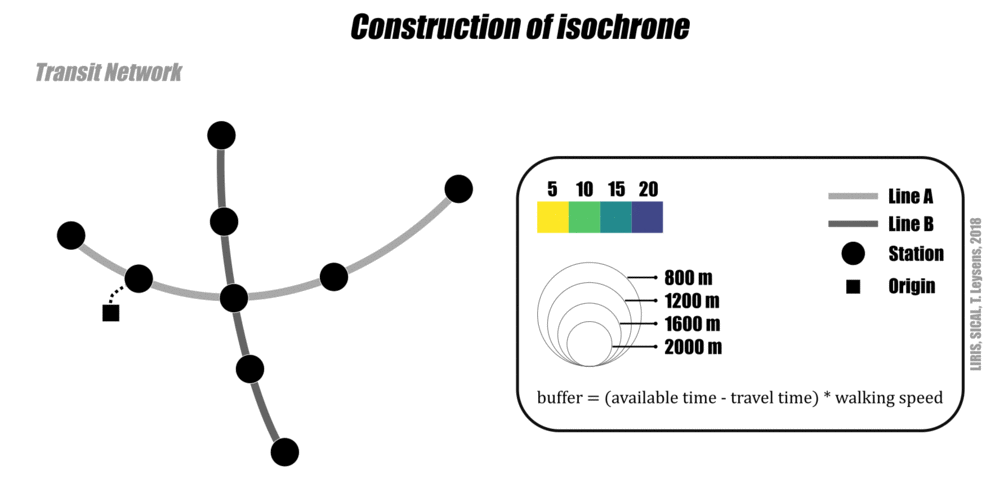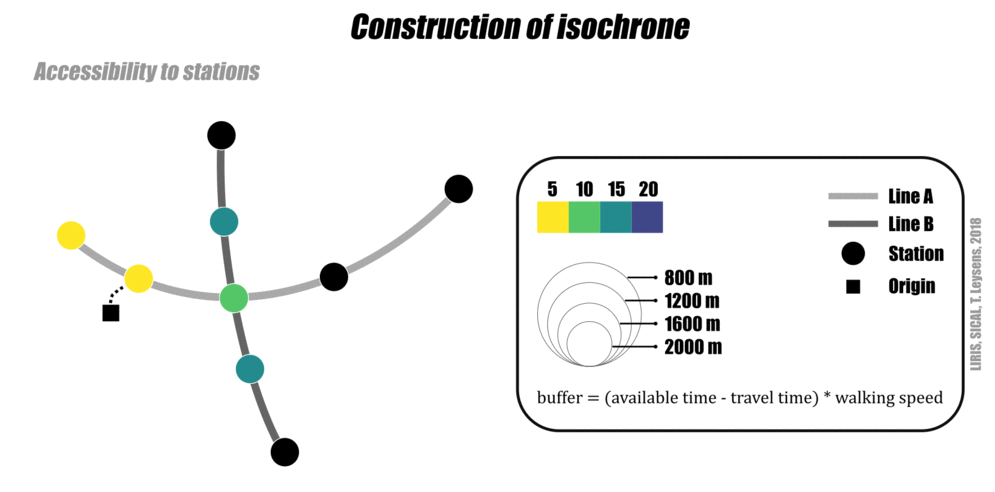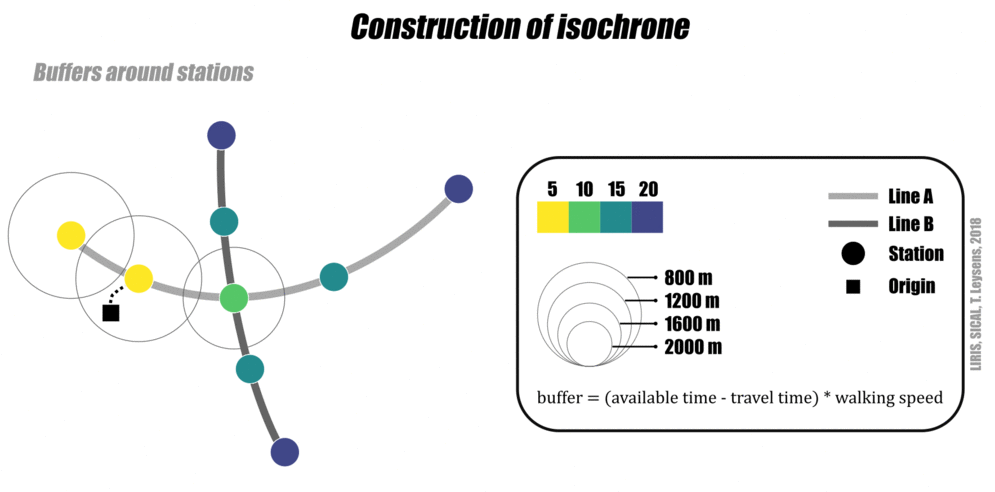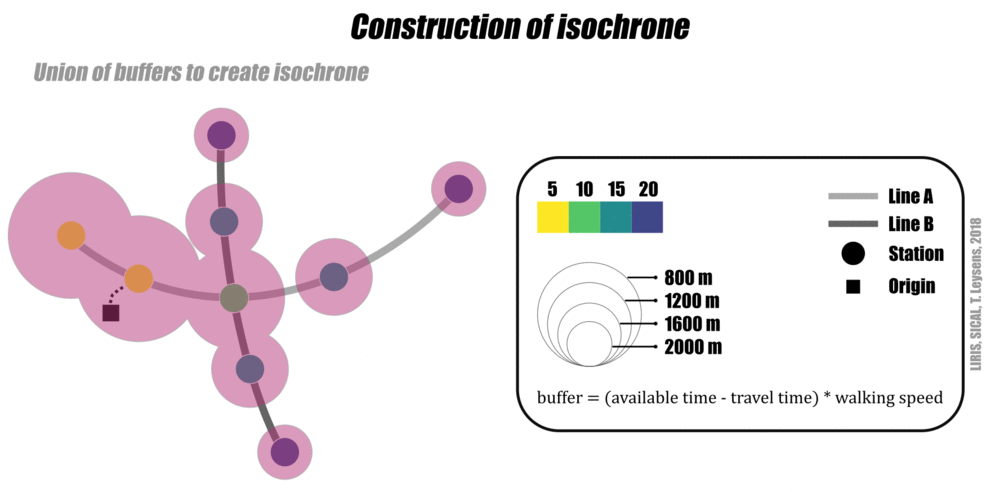
Le graphe et les mesures de l’accessibilité permettent d’élaborer des isochrones de transports collectifs et de marche à pied:

  • on calcule les nœuds accessibles depuis un nœud d’origine dans un temps donné
  • on déduit du temps maximum la durée de déplacement pour avoir un temps restant
  • ce temps disponible sert à calculer un périmètre d’accessibilité à pied (en fonction d’une vitesse moyenne) autour de chaque nœud accessible (ce périmètre peut prendre la forme d’un cerle à vol d’oiseau ou d’un polygone contraint par le réseau viaire).

Approche schématique

L’animation suivante montre l’élaboration d’un isochrone (transports collectifs et marche à pied) de manière schématique.

Exemple cartographique

L’animation ci-après montre une cartographie réalisée dans un notebook Jupyter (notamment avec la librairie Python Bokeh)

Elle montre la différence entre l’accessibilité théorique (un cercle de 20 minutes à une vitesse moyenne théorique de 20 km/h - source - en transports collectifs) et un isochrone construit selon la méthode exposée précédemment (avec quelques variations que nous expliquerons dans un autre billet de blog). L’animation vise à montrer rapidement - et de manière très simplifiée - la construction de l’isochrone.

Et donc ?

En croisant spatialement cette zone d’accessibilité réelle avec, pour reprendre notre exemple des restaurants, une base de données des restaurants, il devient simple de repérer en un seul coup d’oeil les établissements réellement accessibles en tenant compte de toutes les contraintes spatio-temporelles. Il est également possible de procéder à beaucoup d’autres opérations spatiales mais nous verrons cela dans un prochain billet de blog.