Context

In many applicative areas such as engineering, numerical simulations, fabrication, or material sciences, modeling geometrical objects and performing numerical analysis have become the cornerstone of many design processes or decision-making strategies. The aim of the StableProxies project is to provide high-performance and stable geometry processing tools to perform reliable numerical computations on generic geometrical objects.

In the project, we address a large class of discrete geometrical structures that may be used for the simulation of physical phenomena. Depending on the acquisition or design process, and on the application constraints, various data structures coexist to describe 3D shapes. Discrete meshes approximate surfaces using piecewise linear or higher order elements with sometimes incorrect topological information. They are widely used in engineering and computer graphics (see Fig 1-(a-b)).

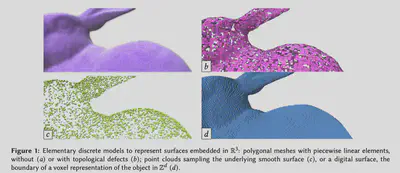
Many capture devices or processes generate point clouds (e.g., LiDAR, SfM reconstruction from images) with no connectivity but with increased resolution (Fig 1-(c)). Volumetric objects composed of voxels classically arise from medical imaging or material sciences (Fig 1-(d)). Aside from the models, the numerical computations we are targeting mainly involve differential quantities and variational problems. For instance, we could be interested in estimating stable differential quantities (curvature, normal vectors…) from point clouds, meshes or digital surfaces (cf Fig. 2- (a-c)), solve some partial differential equations (Poisson problems) to estimate shortest paths on surfaces (cf Fig. 2-(d)), or to estimate heat flow in fibrous materials (cf Fig. 2-(e)) ; or use variational formulations for shape optimization (e.g., membranous material design Fig. 2-(f), or fracture simulation Fig. 2-(g)).

Objectives

Motivated by the diversity of possible representations of geometrical data and the need to provide tools to process them, the main overall objective of the StableProxies project is to provide theoretically stable and efficient tools to perform high-performance geometric computations on complex, heterogeneous and defective discrete geometrical data. The core research hypothesis of the StableProxies project is to rely on the notion of a geometrical proxy capturing the geometry of the input data, and on which the computations are performed. We further aim at stability properties as we are interested in providing accuracy guarantees for the approximation induced by the proxy, and the numerical computations computed on it. Such a proxy must balance several objectives. First, it must be versatile enough to approach data with complex topology, so not only surfaces, but also curves or networks, union of surfaces with non-manifold crossing lines, point clouds or even volumetric partitions. To do so, the proxy should be a cellular model with incidence relations, enabling the representation of generic shapes with enough topology for a later calculus. Second, it must be accurate to approach data with arbitrary precision. This entails that the proxy has a controllable sampling refinement, possibly variable, with theoretical accuracy guarantees. Third, it must be compact both to save memory usage, to offer dedicated data structures and to speed up lookup and computation algorithms. Grids and dyadic grids are suited to this constraint, since they can encode both implicit shape description or explicit axis-aligned cells with incidence relations in a compact way. Fourth, they must be algebraically expressive to allow consistent differential calculus operators onto the structure (gradient, vector fields, etc), with some accuracy guarantees.

For all those reasons, we claim that the digital model (subsets of Z𝑑, or subsets of the cellular decomposition of Z𝑑 ) is a good candidate for high-performance and reliable geometrical computations. Embedding the computations on a cellular grid would provide fast computations from dedicated data structure, the ability to represent objects and structures with various dimensions in the same model, and a topological support from the ambient space. This research hypothesis raises many challenges addressed by the StableProxies project:

• First, for the targeted geometry processing applications, we need high-end differential estimators or numerical schemes for discrete variational problems on surfaces. Furthermore, to set up the proxy model, we need a generic mathematical framework from which stability results can be obtained for various discrete object settings (WP1).
• We need to design a digital proxy model for generic discrete data (meshes, point clouds, triangle soups) from which stability results could be obtained. This implies both transfer operators with guarantees, as well as investigating additional embedding information (density, normal bundle…), that could be attached to the digital proxy to achieve the stability of the computations (WP2).
• High-performance computations on the digital proxy model would benefit from the regular nature of the digital geometry model. Beside efficient data structures to represent regularly spaced data or cellular information, a key challenge would be to design differential estimators, or multigrid solvers specifically suited to that model (WP3).
• Finally, the StableProxies project will investigate several application scenarii demonstrating the relevance of using a generic model to perform geometry processing tasks on unstructured data (LiDAR point clouds) or high resolution volumetric objects (Material Sciences), as well as to solve complex shape optimization problems. (WP4).