Multigrid intrinsic solver for digital surfaces -- Master 2 Internship proposal

https://codimd.math.cnrs.fr/s/S0ih2B5un

Contexte

In many applicative areas such as engineering, numerical simulations, fabrication, or material sciences, modeling geometrical objects and performing numerical analysis have become the cornerstone of many design processes or decision-making strategies. The aim of the StableProxies project is to provide high-performance and stable geometry processing tools to perform reliable numerical computations on generic geometrical objects. In the project, we address a large class of discrete geometrical structures that may be used for the simulation of physical phenomena. Depending on the acquisition or design process, and on the application constraints, various data structures coexist to describe 3D shapes. Discrete meshes approximate surfaces using piecewise linear or higher order elements with sometimes incorrect topological information. They are widely used in engineering and computer graphics (see Fig(a-b)).

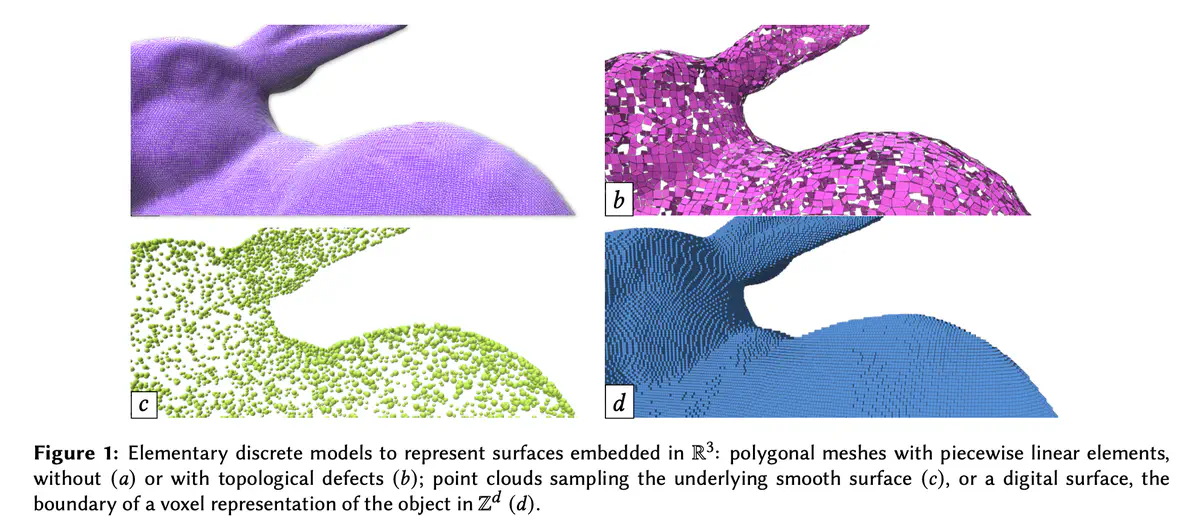
The main overall objective of the StableProxies project is to provide theoretically stable and efficient tools to perform high-performance geometric computations on complex, heterogeneous and defective discrete geometrical data.

We claim that the digital model (subsets of $\mathbb{Z}^𝑑$, or subsets of the cellular decomposition of $\mathbb{Z}^𝑑$) is a good candidate for high-performance and reliable geometrical computations. We aim at developing robust geometry processing tools using a digital proxy model.

Multigrid intrinsic solver for digital surfaces

When solving a complex variational problem on large domains, multigrid solvers define a wide range of methods to efficiently solve the problem on low-resolution domains, with prolongation operators to the finer resolutions. For structured domains (grids), many solutions exist ¹. Many geometry processing problems can be cast as positive (semi-)definite problems on discrete surfaces (parameterization, geodesics, fairing. . . ). For manifold meshes, recent approaches aim to define Galerkin geometric multigrid solvers that can be used as a black box to solve linear problems ².

For digital surfaces, the defective embedding of the geometry makes such intrinsic Galerkin scheme not optimal. On the other hand, trivial multigrid schemes exist for the grid supporting the digital surface definition. The objective of this task is to propose a new intrinsic-ambient multigrid solver for the high performance geometry processing on digital surfaces. As depicted in the following Figure

one way to address the problem would be to construct a multigrid scheme (and its prolongation operator) that would be consistent with the digital surface of the underlying object on the upscaled/downscaled grids. In this task, adaptive resolution representation of digital surfaces will also be investigated with the objective of designing efficient numerical solvers for solving PDE on surfaces. For instance, following ³⁴, can a complete corrected discrete calculus on adaptive digital surfaces be designed while preserving the accuracy of the computations?

References