Continuous maps between heterogeneous data (point cloud, meshes) and digital proxies -- Master 2 Internship proposal

https://codimd.math.cnrs.fr/s/S0ih2B5un

Contexte

In many applicative areas such as engineering, numerical simulations, fabrication, or material sciences, modeling geometrical objects and performing numerical analysis have become the cornerstone of many design processes or decision-making strategies. The aim of the StableProxies project is to provide high-performance and stable geometry processing tools to perform reliable numerical computations on generic geometrical objects. In the project, we address a large class of discrete geometrical structures that may be used for the simulation of physical phenomena. Depending on the acquisition or design process, and on the application constraints, various data structures coexist to describe 3D shapes. Discrete meshes approximate surfaces using piecewise linear or higher order elements with sometimes incorrect topological information. They are widely used in engineering and computer graphics (see Fig(a-b)).

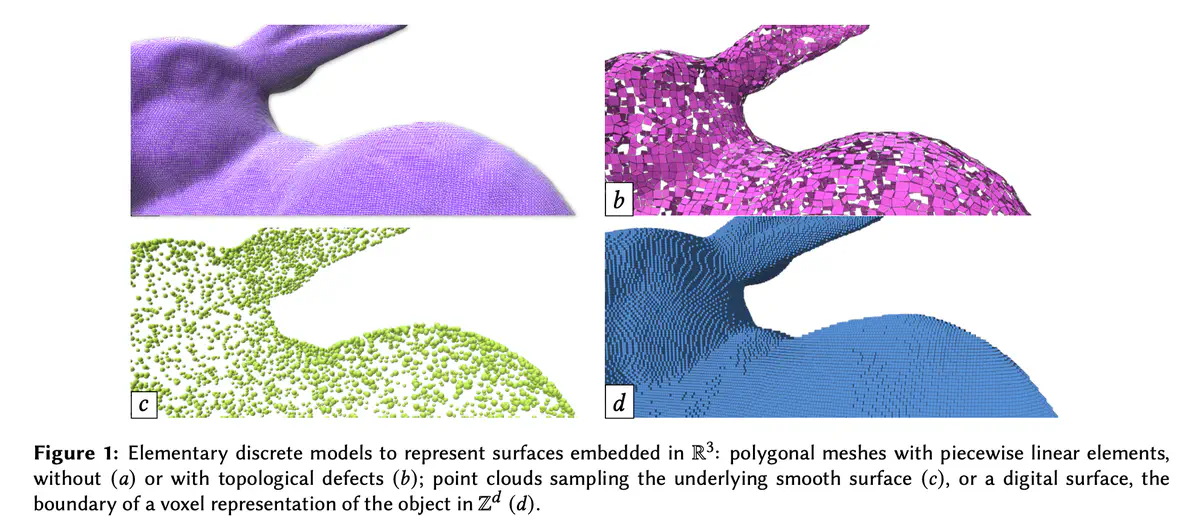
The main overall objective of the StableProxies project is to provide theoretically stable and efficient tools to perform high-performance geometric computations on complex, heterogeneous and defective discrete geometrical data.

We claim that the digital model (subsets of $\mathbb{Z}^𝑑$, or subsets of the cellular decomposition of $\mathbb{Z}^𝑑$) is a good candidate for high-performance and reliable geometrical computations. We aim at developing robust geometry processing tools using a digital proxy model.

Continuous maps between heterogeneous data (point cloud, meshes) and digital proxies

As mentioned above, the goal of the Stable Proxies project is to be able to run numerical simulations on heterogeneous data : the input data can be point clouds, voxels or surface meshes, sometimes faulty with outliers (points resulting from measurement errors during an acquisition process for instance) or connectivity issues (cracks in the surface, self-intersections for instance). Numerical simulations on the contrary require nicely meshed domains : triangle or tetrahedral meshes for finite elements, with requirements on the shape of the triangles to ensure the convergence of the simulation, or even regular grids. Our goal is therefore to design a proxy object matching the quality requirements to run numerical simulations, but also closely related to the input faulty data. We also need a mapping to transfer attributes from the input data to the proxy to initialize the simulation, and back to recover the result of the simulation.

This subject aims at both constructing the proxy and defining its mapping with the input data. The designed proxy has to be suitable for numerical simulations and to accurately match the input data in terms of position, normal vectors and curvatures. As mentioned above, a digital model could be a suitable choice of proxy ¹. Designing the correct digital model for a given input data remains a challenge, in particular to automatically detect the dimensionality of the input data and use a grid resolution accurate enough for the input data but also tractable in terms of numerical simulation. Remeshing for simulation is still an active field of research ² and handling mesh quality is one of the most challenging problems of the field. A closely related approach for instance is the polycube maps approach mapping the input data to a subset of $\mathbb{Z}^𝑑$

Image courtesy of C.Dumery et al. ³

When mapping between the proxy and the input data, classical baking techniques usually use the nearest point interpolation or matching parameterizations of both the source and target. Parameterization can be a challenging problem on faulty data and the nearest point interpolation can lead to artifacts : attributes being mapped to several parts of the target object, or attributes of the input object not mapped to anything on the target. Designing maps between shapes is a classical problem in computer graphics ⁴, ⁵. Another possible research track could be the use of optimal transport (e.g. ⁶) to ensure that all the input samples are mapped to the target with a resolution matching that of the input sampling. This would involve discrete-discrete optimal transport algorithms for instance when approximating a point cloud with a voxel proxy with a limited number of corrected normals. Semi-discrete algorithms will also be considered when building a proxy from non-manifold surfaces (like soup of triangles). Optimal setting of the normal vector field for a given proxy voxel geometry could also be considered. While building a mapping, an important challenge would be to keep track of topological properties, or inferred topological properties (e.g., dimension inference).

References