OutilsMaths - Python¶
Bastien DOIGNIES - Outils Maths LIRIS / ORIGAMI - 12/02/2024
Ce notebook / slideshow présente quelques tips, tricks et idiomes pour le language Python. Le but étant de présenter certaines façons d'utiliser le language, afin d'avoir une meilleure compréhension, rapidité d'execution et fluidité dans le processus de développement.
La présentation est en 3 parties :
- Native python : présente les quelques idiomes python très utilisés qui sont des fonctionnalités "natives" du language.
- Tensor libraries : présente les opérations
numpyqui sont à la base de toutes les librairies manipulant des tableaux (tf, torch, jax, ...) - Performant python : quelques tips & tricks qui permettent d'avoir un code qui tourne plus vite.
Native Python¶
Function parameters and expansions¶
Les fonctions sont des éléments essentiels de tous les languages de programmation. En tant que language non typé, le python offre de nombreuses possibilités en ce qui concerne les fonctions. Il y a deux types d'arguments : positionnels, et nommés.
Les arguments positionnels:
- Se sont les arguments qui doivent être fournis dans l'ordre de la fonction.
- Sont toujours 'les premiers' dans la liste des arguments d'une fonction.
- Une '*' marque la fin des arguments 'positionnels'. Tout ceux d'après doivent OBLIGATOIREMENT être 'nommés'.
- Ils peuvent (ou non) être nommés. En revanche, dès que l'un est nommé, tout ceux d'après doivent aussi l'être.
Les arguments nommés:
- Sont les arguments pour lesquels on spécifie le nom lors de l'appel.
- Pour certains, le nom est obligatoire.
- Puisqu'ils sont nommés, il n'y a pas d'ordre !
def une_fonction1(arg_1, arg_2=10, *, kw_1, kw_2="hello"):
print(arg_1, arg_2, kw_1, kw_2)
une_fonction1(1, 2, kw_1=3, kw_2=4) # tout est spécifié
une_fonction1(1, kw_1=3, kw_2=4) # default for arg_2
une_fonction1(1, kw_1=3, arg_2=4) # No order when named
1 2 3 4 1 10 3 4 1 4 3 hello
# 3, et 4 corresponded à kw_1, kw_2 => Ils doivent être nommés
une_fonction1(1, 2, 3, 4)
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) Input In [2], in <cell line: 2>() 1 # 3, et 4 corresponded à kw_1, kw_2 => Ils doivent être nommés ----> 2 une_fonction1(1, 2, 3, 4) TypeError: une_fonction1() takes from 1 to 2 positional arguments but 4 were given
# pos_1 est nommé, tout ceux d'après doivent donc l'être !
une_fonction1(arg_1=1, 2, kw_1=3, kw_2=4)
Input In [3] une_fonction1(arg_1=1, 2, kw_1=3, kw_2=4) ^ SyntaxError: positional argument follows keyword argument
En python, les fonctions peuvent nativement prendre "une infinité" de paramètres. Pour cela, on utilse (par convention), les notations : *args et **kwargs.
*args: Spécifie une 'infinité' d'arguments positionnels (qui ne peuvent donc pas être nommés). Cela marque aussi la fin des arguments positionnels, tous les arguments doivent être nommés. Il s'agit d'un tuple.*kwargs: Est la contrepartie pour les arguments 'nommés'. Il s'agit d'un dictionnaire.
def une_fonction2(pos_1, *args, toto, **kwargs):
print("Normal args: ", pos_1, ",", toto)
print("Positional arguments: ", args)
print("Keyword arguments: ", kwargs)
une_fonction2(1, 2, 3, tata=12, toto="bonjour")
Normal args: 1 , bonjour
Positional arguments: (2, 3)
Keyword arguments: {'tata': 12}
Parfois, il se peut que nos arguments soient rangés dans des listes ou dictionnaires que l'on souhaite envoyer à une fonction en tant que paramètres indépendants. Pour cela, il existe les opérateurs d'expansion : *, **.
params=[1, 2, 3]
kw_args={"toto": 123, "tata": 17}
une_fonction2(params, kw_args, toto="17")
print("----")
une_fonction2(*params, **kw_args) # une_fonction2(1, 2, 3, toto=123, tata=17)
Normal args: [1, 2, 3] , 17
Positional arguments: ({'toto': 123, 'tata': 17},)
Keyword arguments: {}
----
Normal args: 1 , 123
Positional arguments: (2, 3)
Keyword arguments: {'tata': 17}
Context managers¶
L'utilisation des context managers est assez courrante en python, sans que le nom ne soit pour autant pronnoncé. Le but est de gérer des ressources, principalement lors de la création d'une ressource dont la supression est nécessaire. L'exemple courant est l'utilisation de fichiers. Les context managers s'utilisent avec la close with.
with open("file1.txt") as file:
print(*file.readlines())
Je suis du texte dans un fichier Deuxième ligne
Ce bout de code est en fait équivalent à un simple try/finally. Il sagit principalement d'un sucre syntaxique.
try:
file = open("file1.txt")
print(*file.readlines())
finally: # Always executed, no matter if an exception occurs or not
file.close()
Je suis du texte dans un fichier Deuxième ligne
L'implémentation d'un objet supportant ce type est très simple. Il suffit de surcharger les fonctions __enter__, et __exit__.
class FileWrapper:
def __init__(self, file_name, method):
self.file_obj = open(file_name, method)
def __enter__(self):
return self.file_obj # Returns the 'classic python file'
def __exit__(self, type, value, traceback_):
if value:
print(f"{type}: {value}")
import traceback
print(traceback.format_tb(traceback_)[0])
print("Closing file now")
self.file_obj.close()
return True # Execption is handled. False would rethrow
with FileWrapper("file1.txt", "rt") as file:
raise ValueError("A random error")
<class 'ValueError'>: A random error
File "/tmp/ipykernel_17413/2219059811.py", line 16, in <cell line: 15>
raise ValueError("A random error")
Closing file now
Decorators¶
Les decorators sont des fonctions qui prennent en paramètre une fonction ou une classe, et, éventuellement des arguments, afin d'en modifier le comportement. Ils s'utilisent comme des annotations et ne sont, là encore, qu'un sucre syntaxique.
Exemple d'utilisation :
from dataclasses import dataclass
@dataclass # Rajoute: constructeur, egalités, print, ...
class Student:
name: str
avg_grades: float
st1 = Student("Toto", 5.0)
st2 = Student("Tata", 10.0)
print(f"{st1}, {st2}, IsSame?: {st1 == st2}")
Student(name='Toto', avg_grades=5.0), Student(name='Tata', avg_grades=10.0), IsSame?: False
Exemple de création d'un décorateur qui est bien utile !
import time
def time_function(func):
def time_wrapper(*args, **kwargs):
start_time = time.perf_counter()
result = func(*args, **kwargs) # Execute la fonction
end_time = time.perf_counter()
total_time = end_time - start_time
print(f'Function {func.__name__}{args} {kwargs} Took {total_time:.4f} seconds')
return result
return time_wrapper
@time_function
def hello_world(str):
time.sleep(2.0)
print(str)
hello_world("Param")
Param
Function hello_world('Param',) {} Took 2.0022 seconds
L'idée d'un decorateur est ainsi "d'intercepter" une fonction ou un objet, pour en renvoyer une autre à la place. Quelques decorateurs utiles :
abc.abstractmethod: decorateurs pour faire des méthodes abstraitesstaticmethod: fonctions statiques (comme en C++)functools.wraps: permet de forward les noms, documentations, ... des fonctions retournées.functools.cache: cache les valeurs de retours d'une fonctionfunctools.total_ordering: Etant donner un opérateur de comparaison pour une classe, complète les autres.dataclasses.dataclass: utilitaire pour construire des classes rapidement
Librairies externes:
numpy.vectorize: Permet à une fonction de prendre un tableau en paramètre (mais n'optimise pas le code pour du SSE)numba.jit,jax.jit,tf.function,torch.jit: Permet de compiler une fonction pour accélerer son execution.
Generators¶
Les générateurs représentent des séquences qui ne sont évaluées que de manière "paraisseuses". Le générateur le plus connu est range.
for i in range(1000):
pass # Do something with i
Tous les entiers de 0 à 999 ne sont pas mis dans une liste. A la place ils sont 'générés uns par uns'. Cela permet d'éviter une construction mémoire. C'est l'équivalent des coroutines dans pas mal de language (co_yield, co_return en C++). Ils s'utilsent dans une boucle, ou avec l'instruction next. La fin est signalée par une exception StopIteration.
def fibonacci():
a=0
b=1
for i in range(6):
yield b
a, b = b, a + b
for fibo in fibonacci():
print(fibo, end=' ')
1 1 2 3 5 8
gen = fibonacci()
print(next(gen), next(gen), next(gen), next(gen), next(gen), next(gen))
print(next(gen))
1 1 2 3 5 8
--------------------------------------------------------------------------- StopIteration Traceback (most recent call last) Input In [14], in <cell line: 3>() 1 gen = fibonacci() 2 print(next(gen), next(gen), next(gen), next(gen), next(gen), next(gen)) ----> 3 print(next(gen)) StopIteration:
List / Dict / Generator comprehension¶
Apparues dès le début de Python 2, les compréhensions offrent de puissants outils de création de listes, dictionnaires et de générateurs. La puissance vient principalement de la rapidité d'éxéctution du code: l'interpreteur python est capable de compiler le code pour l'éxécuter plus vite.
[i ** i for i in range(6)] # Une liste
[1, 1, 4, 27, 256, 3125]
{float(i): i ** i for i in range(6)} # Un dictionnaire
{0.0: 1, 1.0: 1, 2.0: 4, 3.0: 27, 4.0: 256, 5.0: 3125}
(i ** i for i in range(6)) # Un générateur : rien n'a été évalué !
<generator object <genexpr> at 0x7f5f7209cdd0>
Il est également possible d'appliquer des filtres et de composer les expressions:
[i ** i for i in range(6) if i % 2 == 0]
[1, 4, 256]
[{k: i for k in range(-3, 2)} for i in range(5) if i % 2 == 0]
[{-3: 0, -2: 0, -1: 0, 0: 0, 1: 0},
{-3: 2, -2: 2, -1: 2, 0: 2, 1: 2},
{-3: 4, -2: 4, -1: 4, 0: 4, 1: 4}]
une_fonction2(
*[i ** i for i in range(5)],
**{f"t{c}t{c}": ord(c) for c in 'aeiou'}
)
Normal args: 1 , 111
Positional arguments: (1, 4, 27, 256)
Keyword arguments: {'tata': 97, 'tete': 101, 'titi': 105, 'tutu': 117}
Important à noter : les compréhension ré-évaluent les expressions à chaque fois :
a = [[]] * 5 # Liste de 5 listes vides
b = [[] for _ in range(5)] # Liste de 5 listes vides
a[0].append(10)
b[0].append(10)
print(a) # a est en fait une liste de références
print(b) # b est une liste de liste différentes
[[10], [10], [10], [10], [10]] [[10], [], [], [], []]
Tensors manipulations¶
Shape and definition.¶
Un tenseur est simplement un tableau n-d de valeurs. De nombreuses librairies permettent de les manipuler : numpy, pytorch, tensorflow, jax, ... Ici, on ne se concentre que sur numpy, qui est la plus utilisée et celle qui a historiquement défini les interfaces ainsi que les façons de manipuler les tableaux.
import numpy as np
a = np.random.uniform(0, 1, (4, 8, 12, 24)) # 9216
print(a.ndim, a.shape) # Nombre de dimension, taille
print(a.dtype, a.nbytes) # Type, occupation mémoire
4 (4, 8, 12, 24) float64 73728
Pour information un tableau numpy est limité à 32 dimensions et 232 éléments.
Il est possible de changer la taille d'un tableau ainsi que son type. Pas de contrainte entre les types, cela marche "comme les casts" en C. En ce qui concerne la taille, il faut que tout soit compatible.
b = a.astype(int) # Floats entre [0, 1] => Tableau de 0 !
c = a.reshape((4 * 8, 12 * 24)) # Change la taille
d = a.reshape(123456)
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) Input In [23], in <cell line: 3>() 1 b = a.astype(int) # Floats entre [0, 1] => Tableau de 0 ! 2 c = a.reshape((4 * 8, 12 * 24)) # Change la taille ----> 3 d = a.reshape(123456) ValueError: cannot reshape array of size 9216 into shape (123456,)
Slicing, strides and views¶
Il est utile de savoir manipuler les éléments des tableaux. Pour ce faire, il faut indexer les éléments. On accède aux éléments d'un tableau avec l'opérateur "classique".
a = np.random.uniform(0, 1, (100, 100))
print(a[0].shape) # Première ligne
print(a[0][1], a[0, 1]) # Deuxième élément de la première ligne
(100,) 0.09699281353192157 0.09699281353192157
Le slicing consiste à prendre des parties d'un tableau. L'opérateur de slicing s'écrit avec des ':' avec la syntaxe: début[0]:fin[N]:increment[1]. Le début est inclu, la fin est exclue.
a = np.arange(10)
print(a)
print(a[3:])
print(a[:7])
print(a[::2])
[0 1 2 3 4 5 6 7 8 9] [3 4 5 6 7 8 9] [0 1 2 3 4 5 6] [0 2 4 6 8]
a = np.arange(100).reshape((10, 10))
print(a[:3, ::2])
print(a[::2, 2:8:2])
[[ 0 2 4 6 8] [10 12 14 16 18] [20 22 24 26 28]] [[ 2 4 6] [22 24 26] [42 44 46] [62 64 66] [82 84 86]]
En python les indices négatifs permettent d'indexer à partir de la fin d'un tableau. Cela peut être utilisé dans les slices :
a = np.arange(10)
print(a[-1], a[-2], a[-3])
print(a[::-1])
print(a[-6::-1], a[a.shape[0]-6::-1])
print(a[:-3], a[:a.shape[0]-3])
9 8 7 [9 8 7 6 5 4 3 2 1 0] [4 3 2 1 0] [4 3 2 1 0] [0 1 2 3 4 5 6] [0 1 2 3 4 5 6]
Les tableaux numpy sont stockés sous forme de buffers linéaires. Les opérations de slicing et de reshape changent seulement la façon de parcourir les éléments et non la mémoire associée : modifier une slice modifie le tableau originel !!!
On appelle stride le tableau d'entiers qui permet de parcourir le buffer linéaire.
a = np.arange(100).reshape((10, 10))
print(a.strides) # En bytes !
print(a[::2, ::2].strides)
print(a.reshape(2, 5, 2, 5).strides)
# La mémoire est partagée
a[::2, ::2][1, 1] = 100
print(a[2, 2])
print(a[::2, ::2].base is a.base)
(80, 8) (160, 16) (400, 80, 40, 8) 100 True
Les tableaux numpy implémentent l'interface python buffer protocol qui permet de lier les structures de données des différentes librairies. En particulier, les tableaux peuvent être utilisés comme des listes ! Ainsi qu'avec l'opérateur d'expansion... :
a = np.arange(10)
for e in a:
print(e, end=' ')
print()
print(*a)
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9
Transpose, swaps and reordering¶
Comme expliqué, l'opération reshape ne réordonne pas les éléments; pourtant, cela peut être pratique de les réordonner. Les images sont courrament chargées sous la forme : (W, H, C); mais la plupart des modules de deep learning attendent un input sous la forme (C, W, H).
import matplotlib.pyplot as plt
img = np.load("img-orig.npy")
plt.imshow(img, cmap="gray")
plt.show()
img = np.load("img-reshape.npy")
plt.imshow(img, cmap="gray")
plt.show()
La transposition permet de renverser les dimensions des tenseurs. Dit autrement: (a, b, c, d, e) -> (e, d, c, b, a). Il n'est jamais clair si une vue ou une copy est retournée.
La documentation dit :
np.transpose<=>ndarray.transposenp.transposeretourne une vue "si possible"ndarray.transposeretourne toujours une vue
La fonction transpose, lorsqu'aucune copie n'est effectuée, ne modifie que les strides.
a = np.random.uniform(0, 1, (3, 5, 6, 7))
print(a.T.shape, a.transpose().shape, a.strides,
a.transpose().strides, a.transpose().base is a)
(7, 6, 5, 3) (7, 6, 5, 3) (1680, 336, 56, 8) (8, 56, 336, 1680) True
Il est possible de n'inverser que quelques axes en les spécifiant à la fonction np.transpose, ou en utilisant la fonction np.swapaxes
print(a.shape, np.transpose(a, axes=[2, 0, 1, 3]).shape,
np.swapaxes(a, 2, 3).shape)
(3, 5, 6, 7) (6, 3, 5, 7) (3, 5, 7, 6)
Il peut aussi être utile de modifier l'ordre dans lequel sont parcourrues les données d'un axe. Cela peut par exemple être utile pour convertir des données au format BGR vers le format RGB. Cependant, une copie sera effectuée.
img = np.random.uniform(0, 1, (2, 2, 3))
print(img, end='\n------\n')
print(img[:, :, [2, 1, 0]])
print(img[:, :, [2, 1, 0]].base is img)
[[[0.79837192 0.6188082 0.23601781] [0.98645274 0.71349537 0.85564159]] [[0.448892 0.27675856 0.77261651] [0.15859153 0.66546963 0.90570064]]] ------ [[[0.23601781 0.6188082 0.79837192] [0.85564159 0.71349537 0.98645274]] [[0.77261651 0.27675856 0.448892 ] [0.90570064 0.66546963 0.15859153]]] False
Il est ainsi possible d'indexer un tableau par un autre tableau, dans ce cas, il faut penser que l'on fait des permutations des lignes et colonnes selectionnées. a[b] = [a[b[0]], a[b[1]], ..., a[b[-1]]]. Le tableau qui sert d'index peut contenir plusieurs fois les mêmes valeur.
a = np.random.uniform(0, 1, (3, 3))
b = np.mod(np.arange(6), 3)
print(a, end='\n-----\n')
print(a[b], end='\n-----\n')
print(a[b, b]) # a[b[0], b[0]], ...
[[0.92843087 0.28977279 0.46622837] [0.44286041 0.28848803 0.86780291] [0.61255275 0.76783121 0.95824636]] ----- [[0.92843087 0.28977279 0.46622837] [0.44286041 0.28848803 0.86780291] [0.61255275 0.76783121 0.95824636] [0.92843087 0.28977279 0.46622837] [0.44286041 0.28848803 0.86780291] [0.61255275 0.76783121 0.95824636]] ----- [0.92843087 0.28848803 0.95824636 0.92843087 0.28848803 0.95824636]
Il faut cependant faire attention à la signification de l'indexation lorsque le tableau utilisé est multidimentionnel :
a = np.random.uniform(0, 1, (4, 3))
b = np.random.randint(0, 4, (5, 5))
print(a, end='\n------\n')
print(b, end='\n------\n')
print(a[b].shape) # (b.shape[0], b.shape[0], a.shape[1])
print(a[b]) # [[a[b[0, 0], :], a[b[0, 1], :], ...],
# [a[b[1, 0], :], a[b[1, 1], :], ...],
# ...]
[[0.39837793 0.16433895 0.25441618] [0.16983742 0.78703155 0.55759947] [0.74368042 0.31835569 0.5106531 ] [0.09724865 0.25062777 0.92992606]] ------ [[0 0 0 3 0] [0 2 1 3 3] [3 3 1 1 2] [3 3 1 1 1] [0 1 1 1 0]] ------ (5, 5, 3) [[[0.39837793 0.16433895 0.25441618] [0.39837793 0.16433895 0.25441618] [0.39837793 0.16433895 0.25441618] [0.09724865 0.25062777 0.92992606] [0.39837793 0.16433895 0.25441618]] [[0.39837793 0.16433895 0.25441618] [0.74368042 0.31835569 0.5106531 ] [0.16983742 0.78703155 0.55759947] [0.09724865 0.25062777 0.92992606] [0.09724865 0.25062777 0.92992606]] [[0.09724865 0.25062777 0.92992606] [0.09724865 0.25062777 0.92992606] [0.16983742 0.78703155 0.55759947] [0.16983742 0.78703155 0.55759947] [0.74368042 0.31835569 0.5106531 ]] [[0.09724865 0.25062777 0.92992606] [0.09724865 0.25062777 0.92992606] [0.16983742 0.78703155 0.55759947] [0.16983742 0.78703155 0.55759947] [0.16983742 0.78703155 0.55759947]] [[0.39837793 0.16433895 0.25441618] [0.16983742 0.78703155 0.55759947] [0.16983742 0.78703155 0.55759947] [0.16983742 0.78703155 0.55759947] [0.39837793 0.16433895 0.25441618]]]
Il est aussi possible de sélectionner les éléments avec des tableaux de booléens. Cependant les règles sont légèrement différentes... En particulier, lorsque x.ndim == idx.ndim, seul un tableau 1D est retourné !
a = np.random.uniform(0, 1, (4, 4))
print(a)
print(a > 0.5)
print(a[a > 0.5])
[[0.67082828 0.87703582 0.5809604 0.12740931] [0.7347204 0.52260261 0.38983942 0.34035182] [0.80333285 0.61066083 0.99357265 0.37331473] [0.23527046 0.78415762 0.30598898 0.91661261]] [[ True True True False] [ True True False False] [ True True True False] [False True False True]] [0.67082828 0.87703582 0.5809604 0.7347204 0.52260261 0.80333285 0.61066083 0.99357265 0.78415762 0.91661261]
Broadcasting¶
Le broadcasting est un ensemble de règles qui permettent de faire des opérations termes à termes sur des vecteurs de tailles différentes. On dit que deux dimensions sont compatibles si :
- Elles sont égales
- L'une est égale à 1
Lorsque les conditions sont réunies, le tableau est alors "virtuellement étendu". Il est possible que des tableaux n'aient pas le même nombre de dimensions. Dans ce cas, le plus petit est "étendu" pour commencer par (1, 1, ...).
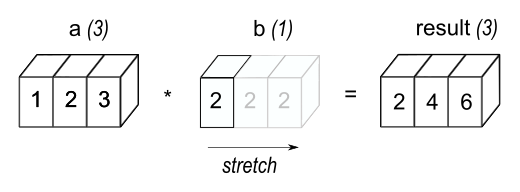
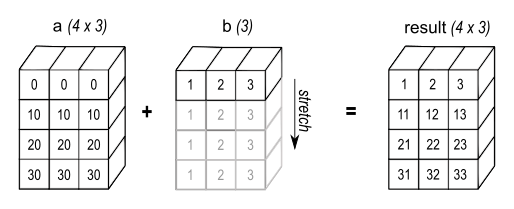
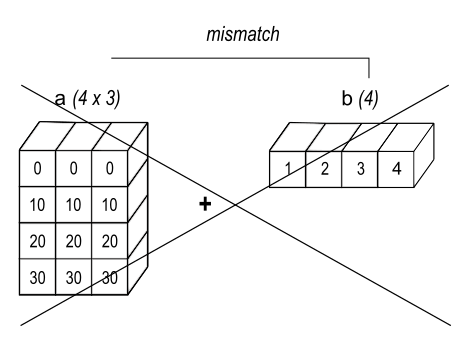
Le broadcasting permet de faire de nombreuses opérations. Notamment les 'outer product' avec une opération quelconque (il y a alors un "double broadcasting") :
a = np.array([0.0, 10.0, 20.0, 30.0])
b = np.array([1.0, 2.0, 3.0])
# a[:, np.newaxis] => (4, 1)
# b => (3)
print(a[:, np.newaxis] * b)
print(np.multiply.outer(a, b))
[[ 0. 0. 0.] [10. 20. 30.] [20. 40. 60.] [30. 60. 90.]] [[ 0. 0. 0.] [10. 20. 30.] [20. 40. 60.] [30. 60. 90.]]
Reduction et Einsum¶
Les libraries qui fonctionnent sur les tenseurs offrent de nombreuses opérations mathématiques (trigo, hyperboliques, ...). La plupart des opérations binaires peuvent être vues comme des opérations de réduction : min/max, +, *, ...
Cependant, il est parfois utile de ne faire la réduction que sur une partie des données. Par exemple, pour convertir une image RGB en nuances de gris, il suffit de faire une moyenne sur l'axe correspondant aux cannaux.
a = np.random.uniform(0, 1, (64, 64, 3))
print(np.mean(a, axis=2).shape) # Moyenne / pixel
print(np.max(a, axis=(0, 1)).shape) # Max par channel
print(np.min(a, axis=-1).shape) # Min / pixel
(64, 64) (3,) (64, 64)
Einsum est une opération très puissante. Elle tire son nom du physicien Einstein, et de (ce que je n'ai pas vérifié) ses notations utilisées pour ses calculs tensoriels. Einsum est une notation pour représenter les opérations qui demandent :
- Transpositions des axes
- Multiplications termes à termes
- Additions des multiplications (réductions)
Ces opérations peuvent être réalisées sur un nombre arbitraire de tenseurs qui sont compatibles avec les opérations demandées.
Les dimensions des opérandes sont représentées par des lettres (par convention : i, j, k, ...). Les opérandes sont quant à elles séparées par des , et le tenseur retourné s'indique après une flèche (au besoin). Les dimensions qui restent identiques peuvent être nommées par des ellipses ....
Les règles sont les suivantes :
- Si une dimension n'apparaît qu'une seule fois : elle n'est pas touchée
- Si une dimension apparaît dans deux opérandes différentes : les dimensions sont multipliées puis sommées
- Si une dimension est répétée dans un même tableau : cela indexe la diagonnale et la somme
Premiers exemples :
np.einsum('i', a): retourne une vue sur anp.einsum('ij->ji', a): transpose anp.einsum('ii', a): trace de anp.einsum('i,i', a, b): produit scalairenp.einsum('ik,kj', a, b): multiplication de matricenp.einsum('ij,kj->ik, a, b) : multiplication avec transposition de b
a=np.array([[0, 1], [2, 3]])
b=np.array([[4, 5], [6, 7]])
print(a @ b, end='\n-----\n')
print(np.einsum('ik,kj', a, b), end='\n-----\n')
print(a @ b.T, end='\n-----\n')
print(np.einsum('ij,kj->ik', a, b), end='\n-----\n')
[[ 6 7] [26 31]] ----- [[ 6 7] [26 31]] ----- [[ 5 7] [23 33]] ----- [[ 5 7] [23 33]] -----
Pour certaines personnes, einsum est une façon plus clair de voir des réordonnement de dimensions et les opérations. Pour voir la puissance de cet opérateur et son utilisation en deep learning : https://einops.rocks/pytorch-examples.html.
Pour info :
- Le backend de pytorch (opt_einsum) compile les expressions pour les accélérer. Mais peuvent être plus lentes ou consommer plus de mémoire...
- Un certain nombre d'opérations sont pré-compilées.
- Trouver l'algorithme 'optimal' de contraction étant donné une expression est NP-hard.
Performant python¶
Anecdotes (CPython)¶
Question: Le python est plus lent que le C++. Quelle preuve avez vous ? Avez vous des chiffres à me donner ?
Petit test : incrémenter un entier. Quel est le coût d'incrémenter un entier ? Quel est le coût d'appeler une fonction ? En C++, on ne se pose pas la question...
Incrémenter et affecter un entier (+=) un entier coûte une dizaine de nanoseconde en C++
L'appel d'une fonction (et affectation) est à peine mesurable en C++
Incrémenter et affecter un entier (+=) un entier coûte une centaine de nanoseconde en Python (x9)
L'appel d'une fonction (et affectation) en python coûte 35 ns (x35)
Et encore, c'est du python 3.11 ou il y a eu un gain de 60% sur les appels de fonctions. (Voir : EuroPython 2022 "How we are making Python 3.11 faster - presented by Mark Shannon").
Enfonçons le clou : quelle est la taille d'un entier ?
En fait, ça dépend de sa valeur. Un entier "petit" fait 24 octets, ou... 28 s'il référence un objet (oui, oui...). Un entier en python peut contenir n'importe quelle valeur entière et donc sa taille croit avec la valeur.
import sys
print(sys.getsizeof(10))
print(sys.getsizeof(10**1000))
print((10).__dir__()) # int are objects !
28 468 ['__new__', '__repr__', '__hash__', '__getattribute__', '__lt__', '__le__', '__eq__', '__ne__', '__gt__', '__ge__', '__add__', '__radd__', '__sub__', '__rsub__', '__mul__', '__rmul__', '__mod__', '__rmod__', '__divmod__', '__rdivmod__', '__pow__', '__rpow__', '__neg__', '__pos__', '__abs__', '__bool__', '__invert__', '__lshift__', '__rlshift__', '__rshift__', '__rrshift__', '__and__', '__rand__', '__xor__', '__rxor__', '__or__', '__ror__', '__int__', '__float__', '__floordiv__', '__rfloordiv__', '__truediv__', '__rtruediv__', '__index__', 'conjugate', 'bit_length', 'bit_count', 'to_bytes', 'from_bytes', 'as_integer_ratio', '__trunc__', '__floor__', '__ceil__', '__round__', '__getnewargs__', '__format__', '__sizeof__', 'real', 'imag', 'numerator', 'denominator', '__doc__', '__str__', '__setattr__', '__delattr__', '__init__', '__reduce_ex__', '__reduce__', '__subclasshook__', '__init_subclass__', '__dir__', '__class__']
L'avez vous vu ?
sys.getsizeof(10) vaut 28... Comme si c'était une référence sur un entier ?
a = 10
b = 10
print(a is b)
True
a = 257
b = 257
print(a is b)
False
a = 257; b = 257
print(a is b) # Can be true or false depending on interpreter
False
Oui oui... En fait, tous les entiers de -5 à 256 sont pré-chargés par l'interpréteur, et le code fait des références sur ce singleton.
Multithreading en Python - GIL n'est pas notre amis¶
Le python ne se multi-thread pas.. C'est la faute à GIL ...! En fait, CPython fonctionne sur un système de "reference counting" et de nombreuses questions se posent sur le maintient d'une telle structure dans un contexte de multithreading. Le principal problème est la performance : un compteur atomique ou un lock sur chaque variable coûte trop cher en temps. Le choix a donc été fait de mettre un lock sur tout l'interpreteur : le Global Interpreter Lock.
- En soit, il n'empêche pas le multithreading. Mais seul un seul thread peut executer du code python.
- Multiprocess lance un nouvel interpreteur à chaque fois en lui faisant passer les données globales.
- Les librairies C/C++ utilisant des objets pythons peuvent "relacher GIL". Cela n'est pas possible en python en revanche. Cependant, il est aussi de leur responsabilité d'aller le chercher une fois qu'il s'est barré !
- Les librairies C/C++ n'utilisant que leurs propres données peuvent utiliser la parrallélisation sans aucun soucis.
Il existe une branche de CPython qui s'appelle : "GILECTOMY". C'est à dire d'enlever GIL de l'interpreter totalement. Cependant, il se trouve que la tâche est très ardue :
- L'acceptation est conditionnée aux performances monothread qui doivent rester identiques (actuellement : dégradation de l'ordre de x20 sur du single thread)
- Il faut que la communauté accepte de changer presque toutes les librairires python
Une façon de faire est de lancer le même script sur des données différentes, via, notamment, les paramètres en ligne de commande. Pour ce faire, je conseille la librairie (native) argparse :
import argparse
parser = argparse.ArgumentParser("nom_du_programme")
parser.add_argument("-s", "--long_opt", type=int, help="help", dest="nom_variable")
parser.add_argument("-f", "--flag", action="store_true")
parser.add_argument("-l", nargs="+", type=int, required=True);
# args = parser.parse_args()
# args.nom_variable, args.flag, args.flag, args.l
Les autres interpréteurs¶
En soit, le language Python n'est pas "lent". Rien dans le standard ne spécifie la façon de gérer la mémoire, les appels de fonctions ou les threads. Il existe de nombreux autres intérpreteurs. Cependant, ils ont tous des spécifités qui peuvent légèrement changer le comportement du code...
- CPython : interpreteur par défaut
- Pypy (Jupyter !): JIT. Garbage Collector, support partiel pour les extensions C. Mais pas de multithreading.
- Pyston : Pypy légèrement plus performant (LLVM + optims).
- Nukita : Compilateur python vers C (WTF ?!)
- IronPython : Python en C# (WTF ?!)
- Jython : Python en Java (WTF ?!)
- JsPython : Python en JavaScript (WTF ?!)
Comment ne pas faire du Python - Python edition¶
Never use loops (ou du moins le moins possible)¶
Sur la plupart des calculs, il n'est pas nécessaire d'avoir une boucle. Le coût est juste trop élevé. Utilisez numpy le plus possible. Les fonctions sont parallélisées et vectorisées.
Exemple : calcul de la discrépance en python.
D(P)=(43)d−2N∑z∈P∏dj=1(3−z2j2)+1N2∑z∈P∑z′∈P∏dj=1(2−max(zi,z′i))
- Python vs NumPy : x100
- Python vs PyUTK (C++): x1000
Pour les personnes qui utilisent pandas, voici l'ordre des performances :
- Extraire les colonnes et faire les manipulations en numpy
- Utiliser les opérations
pandas(+, -, ...) (<=> np dans la plupart des cas) - Utiliser les namespace
pandaspour les données non numériques (.str, .time) - Ré-écrire une colonne avec une compréhension de liste
- Utiliser map / apply
- Faire une boucle sur le dataframe.
Souvent, les points (2, 3) offrent les meilleurs compromis temps de développement / temps d'exécution. Si le dataframe est très gros (en gros: 100000 lignes), un groupby est parfois trop lent avec la méthode pandas. En numpy :
import numpy as np
a = np.random.randint(5, size=(10000, 2)) # 5 Catégories + data aléatoires.
data_sorted = a[a[:, 0].argsort()] # Trie les données par leur groupe
# Recupère la dernière apparition de chaque groupe
group_indices = np.unique(data_sorted[:, 0], return_index=True)[1][1:]
grouped = np.split(a, group_indices) # Split le tableau
print([g.shape[0] for g in grouped])
[2030, 1992, 2030, 1997, 1951]
JIT¶
La compilation "Juste à temps" est aussi un moyen de ne pas faire du python en python. L'idée est qu'une fonction, lorsqu'exécutée pour la première fois est compilée pour accélérer ses performances. Le première appel est bien plus lent... Mais pour des performances largement augmentées par la suite. PyPy et Pyston sont deux interpreteurs qui le font automatiquement.
La plupart des librairies de ML proposent un JIT sous la forme d'un simple décorateur : Pytorch, Tensorflow, Jax & Numba. Cependant, elles ont souvent des limitations sur les opérations et les types de paramètres possibles.

import numba as nb
def Test_python(a,b,c,d):
res=0.
for i in nb.prange(a.shape[0]):
res+=a[i]+b[i]*2.+c[i]*3.+d[i]*4.
return res
@nb.njit(fastmath=False,parallel=True)
def Test_nb(a,b,c,d):
res=0.
for i in nb.prange(a.shape[0]):
res+=a[i]+b[i]*2.+c[i]*3.+d[i]*4.
return res
def Test_np(a,b,c,d):
return np.sum(a+b*2.+c*3.+d*4.)
a = np.random.uniform(0, 1, (1000 * 1000))
%timeit Test_python(a, a, a, a)
487 ms ± 18.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
%timeit Test_np(a, a, a, a)
4.53 ms ± 101 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%timeit Test_nb(a, a, a, a)
284 µs ± 49.8 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
Bringing C++ into python¶
La principale force du python dans son utilisation actuelle est sa capacité à utiliser des librairies provenant d'autres languages, et particulièrement C/C++. C'est ce qui rend le deep learning faisable dans ce language : quelques lignes de python pour les developpeurs , mais des centaines de milliers de lignes "efficaces" pour les ingénieurs concevant les librairies. Cela permet une grande flexibilité : avoir de très bonnes performances avec un language très peu restrictif.
Il est tout à fait possible de compiler un code C "à la main" vers une librairie (.so, .dll) qui sera lu et comprise par un interpreteur. Cependant, cela est plutôt technique et demande de bonnes connaissances sur la structure même de l'interpreteur. La solution la plus simple est d'utiliser une librairie qui simplifie le travail : pybind !
L'installation est relativement simple et pose assez peu de problèmes. Sur le site officiel, vous trouverez même de quoi compiler le code directement avec g++, ou, ce que je recommande, avec CMake.
La déclaration d'un module commence par l'utilisation de la maccro PYBIND11_MODULE
PYBIND11_MODULE(example, m) { // Nom, variable
}
Toutes les opérations seront effectuée sur la variable m, que vous pouvez passer à d'autres fonctions :
int add(int i = 1, int j = 2) {
return i + j;
}
// Ailleurs :
// Nom, pointeur sur la fonction, documentation,
// nom des paramètres et éventuelles valeurs par défaut.
m.def("add", &add, "A function which adds two numbers",
py::arg("i") = 1, py::arg("j") = 2);
Les types des paramètres et des valeurs de retours sont automatiquement inférés. Ils sont aussi convertis automatiquement :
- Objets Python <=> Pointeurs, Reférences
- list <=> std::vector
- tuples <=> std::tuple
- dict <=> std::map
- str <=> std::string
- function <=> std::function
- numpy <=> Eigen, py::buffer, ...
Les conversions marchent dans les deux sens ! Il est possible de désactiver les conversions automatiques au besoin. Il faut notamment faire attention aux durées de vies des éléments, et aux éventuelles copies.
Il est également possible d'exposer des classes C++ en python afin de les manipuler :
class Pet {
public:
Pet(const std::string &name) : name(name) { }
void setName(const std::string &name_) { name = name_; }
const std::string &getName() const { return name; }
private:
std::string name;
};
py::class_<Pet>(m, "Pet")
// Constructor
.def(py::init<const std::string &>())
.def("setName", &Pet::setName) // Fonctions
.def("getName", &Pet::getName) // Fonctions
.def("__repr__", // Marche avec des lambdas
[](const Pet &a) {
return "<example.Pet named '" + a.name + "'>";
}
)
.def_readwrite("name", &Pet::name); // Expose une variable
Sans s'étendre plus, pybind supporte aussi correctement l'héritage : exposer une classe qui en hérite d'une autre d'une part. Mais également le fait d'hériter en Python une classe C++ et d'utiliser cette classe en C++ (via le polymorphisme). Cependant, cela demande plus de travail (côté C++) mais la documentation est assez claire sur le sujet.